Paris accueille pour la première fois une grande exposition dédiée à M.C. Escher, à La Monnaie de Paris, du 15 novembre 2025 au 1er mars 2026.
Ce nom vous dit probablement quelque chose : c’est l’artiste qui a transformé la géométrie et les mathématiques en véritables illusions d’optique.
Ses escaliers qui montent et descendent en même temps, ses formes impossibles, ses mondes où tout semble se transformer sous vos yeux ont marqué la pop culture. Du cinéma ("Le Nom de la Rose", avec sa bibliothèque labyrinthique, ou encore "Inception" et sa cage d'escaliers impossibles), à la publicité, en passant par les pochettes de disques, ou les comics.
Cet artiste a su mêler art, logique et imagination comme personne.
Son style unique continue d’inspirer les artistes, les scientifiques et les amateurs de belles images. Avec plus de 200 œuvres et de nombreuses expériences pour vivre vous aussi de l'intérieur ses illusions d'optiques, l'exposition plonge le public dans l'univers imaginaire et vertigineux de ce génie visionnaire néerlandais, dont l’Art magique a beaucoup à apprendre.
« Relativité » (1953), de M.C. Escher. THE M.C. ESCHER COMPANY/THE NETHERLANDS
Maurits Cornelius Escher, plus célèbre sous le nom de M.C. Escher est né le 17 juin 1898 et mort le 27 mars 1972.
Artiste néerlandais connu pour ses gravures sur bois, ses lithographies ou ses motifs géométriques inspirés de l'art islamique.
Ses œuvres les plus connues représentent des constructions impossibles, des explorations de l'infini, des pavages et des transformations, dédiant les modes habituels de représentation habituels des spectateurs.
Escher était un enfant malade, placé dans une école spécialisée dès l'âge de 7 ans. Ses notes étaient relativement faibles mais il excellait en dessin, discipline dans laquelle il se fit rapidement remarquer.
Il se dirigea donc vers l'architecture et les arts décoratifs (sous la direction de son professeur Samuel Jessurun de Mesquita, qui fut sauvagement assassiné par les nazis en 1944, mais auquel il ne cessa jamais de penser)
A la fin de ses études, il voyagea en Italie d'abord, pays où il découvrit les reliefs vertigineux, les côtes escarpées et les pentes abruptes, en rupture avec "le plat pays" dont il était originaire.
C'est ce sentiment de vertige qu'il n'allait pas tarder à reproduire dans bon nombre de ses toiles.
M.C. Escher (1898-1972), Castrovalva, lithographie, 1930
Puis vint la découverte de l'Islam, où il découvrit l'art islamique, fait de motifs géométriques sculptés dans le bois ou la pierre ou bien encore dans l'art complexe de l'agencement des mosaïques, dont les pièces s'emboîtent astucieusement les unes dans les autres, inversant les concepts de "vide" et de "plein".
Ces premiers éléments nous permettent de nous poser des questions fondamentales dans l'élaboration de notre magie :
-Qui a marqué votre vision de la magie, au point d’en inspirer les moindres éléments ?
- Pour quelle(s) raison(s) avons-nous choisi de pratiquer l'Art magique ? (Étonner, s'étonner, retrouver une part d'enfance, ou compenser...)
- Que cherchons-nous à exprimer en montrant un tour de magie ?
- Par quels moyens pouvons-nous l'exprimer ?
En effet, l'œuvre de M.C. Escher ne se contente pas de reproduire des motifs géométriques, aussi complexes soient-ils, mais il utilise ces derniers pour proposer au spectateur des métaphores visuelles pour des concepts mathématiques abstraits.
Ainsi, symétrie/asymétrie, unité/dualité, réalité/reflet, universalité/relativité, unicité/récursivité, changement de taille, de proportion, ou transformations topologiques ne sont pas sans rappeler les familles d'effets de Winston Freer, allant même jusqu'à dévoiler de nouvelles familles (changement de taille, transformation, inversion- haut/bas, endroit/envers, dessus/dessous, ordre/désordre ou vide/plein)
Escher a rapidement compris que notre esprit ne perçoit pas une forme isolée, il interprète toujours ce qu'il observe comme une figure sur un fond.
Ainsi il devient possible d'inverser le processus, en faisant du fond la figure et de la figure le fond, dans un jeu perceptif continu.
Alors, si nos tours sont reliés entre eux par des transitions scénaristiques, ne serait- il pas possible de réfléchir à faire de ces transitions des numéros à part entière ?
« M.C. Escher, « Mosaic », 1961
Les toiles d'Escher nous font prendre conscience que notre perception est dynamique : nous voyons ce que notre esprit choisit de voir.
On retrouve ce principe dans des toutes telles que "Jour et nuit" ou "Ciel et eau"
M.C. Escher, « Sky and water », 1938.
« Day and Night », 1938, by MC Escher. Collection Gemeentemuseum Den Haag/the MC Escher Company
Dès ses premières œuvres, Escher se concentre sur l'expression de l'espace. Son intérêt croissant pour les mathématiques, la géométrie passe par la fascination pour les sphères, les surfaces réfléchissantes ou les surfaces topologiques, comme le ruban de Möbius (objet à deux faces mais qui, si on l'observe attentivement n'en présente qu'une)
Je ne peux que vous encourager à ce sujet à vous référer à l’article « Boule de cristal » publié sur ce blog.
« Hand with a Reflecting Sphere », 1935, by MC Escher
Vous connaissez probablement ce tour du ruban de papier formant un anneau d'un mètre de diamètre et d'une largeur de 5 cm et qui, lorsqu'il est découpé sur toute sa longueur ne forme plus qu'un très grand anneau (au lieu de deux anneaux séparés) et qui, s'il est lui-même découpé sur toute sa longueur forme cette fois deux anneaux enclavés l'un dans l'autre !)
Pour ce faire, il suffit de donner au ruban une torsion de 180 degrés avant de le "souder".
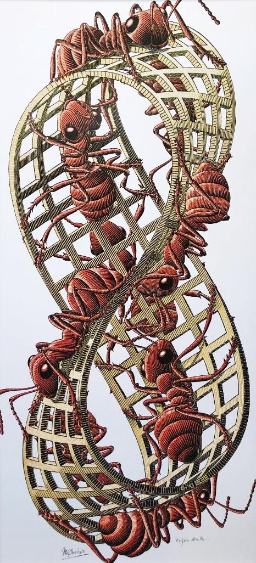
M.C. Escher, « Mobius Strip II (Red Ants) », 1963
Ne reste plus qu'à le découper sur toute sa longueur, deux fois de suite.
Pourquoi pas utiliser des miroirs, des cartes double face ou double dos, des miroirs convexes ou concaves pour permettre à nos spectateurs d’accéder à des formes de réalités impossibles ?
Il utilisa également bon nombre de distorsions, de perspectives, qui, plausibles à première vue, se révèlent impossibles (monter/descendre par exemple) comme dans ses œuvres Relativité ou Belvédère, par exemple)
Ce principe est utilisé dans bon nombre de grandes illusions par exemple pour tromper le public, ou dans des numéros de close up, comme les géniales Gozinta Box (deux boîtes de même dimension, qui rentrent l'une dans l'autre et qui permettent pourtant de faire tenir l'une dans l'autre et pire : la "plus grande" dans la "plus petite" !
Mais plus que tout, si les travaux d'Escher nous touchent tant, c'est parce qu'elles nous montrent d'une manière époustouflante et ludique que des réalités différentes, qui ne sont en réalité que des perceptions différentes, peuvent cohabiter au sein d'une même œuvre.
Alors, ne serait-il pas possible de réfléchir à présenter nos numéros sous un nouveau jour, un autre angle, sous une autre vision ?
"Mon travail est un jeu... Très sérieux. Seuls ceux qui tentent l'absurde peuvent réaliser impossible. Nous aimons le chaos car nous aimons à reproduire l'ordre."
M.C. Escher.
11 quai de Conti - Paris 6e
Ouvert de 10 h à 20 h, du mardi au dimanche. Les mercredis jusqu’à 21h.
Tarifs : A partir de 17€ pour les adultes et à partir de 10€ pour les enfants (gratuit pour les moins de 4 ans)